25.3 Johnson's algorithm for sparse graphs

25.3-1

Use Johnson's algorithm to find the shortest paths between all pairs of vertices in the graph of Figure 25.2. Show the values of $h$ and $\hat w$ computed by the algorithm.

$$ \begin{array}{c|c} v & h(v) \\ \hline 1 & -5 \\ 2 & -3 \\ 3 & 0 \\ 4 & -1 \\ 5 & -6 \\ 6 & -8 \end{array} $$

$$ \begin{array}{ccc|ccc} u & v & \hat w(u, v) & u & v & \hat w(u, v) \\ \hline 1 & 2 & \text{NIL} & 4 & 1 & 0 \\ 1 & 3 & \text{NIL} & 4 & 2 & \text{NIL} \\ 1 & 4 & \text{NIL} & 4 & 3 & \text{NIL} \\ 1 & 5 & 0 & 4 & 5 & 8 \\ 1 & 6 & \text{NIL} & 4 & 6 & \text{NIL} \\ 2 & 1 & 3 & 5 & 1 & \text{NIL} \\ 2 & 3 & \text{NIL} & 5 & 2 & 4 \\ 2 & 4 & 0 & 5 & 3 & \text{NIL} \\ 2 & 5 & \text{NIL} & 5 & 4 & \text{NIL} \\ 2 & 6 & \text{NIL} & 5 & 6 & \text{NIL} \\ 3 & 1 & \text{NIL} & 6 & 1 & \text{NIL} \\ 3 & 2 & 5 & 6 & 2 & 0 \\ 3 & 4 & \text{NIL} & 6 & 3 & 2 \\ 3 & 5 & \text{NIL} & 6 & 4 & \text{NIL} \\ 3 & 6 & 0 & 6 & 5 & \text{NIL} \\ \end{array} $$

So, the $d_{ij}$ values that we get are

$$ \begin{pmatrix} 0 & 6 & \infty & 8 & -1 & \infty \\ -2 & 0 & \infty & 2 & -3 & \infty \\ -5 & -3 & 0 & -1 & -6 & -8 \\ -4 & 2 & \infty & 0 & -5 & \infty \\ 5 & 7 & \infty & 9 & 0 & \infty \\ 3 & 5 & 10 & 7 & 2 & 0 \end{pmatrix} . $$

25.3-2

What is the purpose of adding the new vertex $s$ to $V'$, yielding $V'$?

This is only important when there are negative-weight cycles in the graph. Using a dummy vertex gets us around the problem of trying to compute $-\infty + \infty$ to find $\hat w$. Moreover, if we had instead used a vertex $v$ in the graph instead of the new vertex $s$, then we run into trouble if a vertex fails to be reachable from $v$.

25.3-3

Suppose that $w(u, v) \ge 0$ for all edges $(u, v) \in E$. What is the relationship between the weight functions $w$ and $\hat w$?

If all the edge weights are nonnegative, then the values computed as the shortest distances when running Bellman-Ford will be all zero. This is because when constructing $G'$ on the first line of Johnson's algorithm, we place an edge of weight zero from s to every other vertex. Since any path within the graph has no negative edges, its cost cannot be negative, and so, cannot beat the trivial path that goes straight from $s$ to any given vertex. Since we have that $h(u) = h(v)$ for every $u$ and $v$, the reweighting that occurs only adds and subtracts $0$, and so we have that $w(u, v) = \hat w(u, v)$

25.3-4

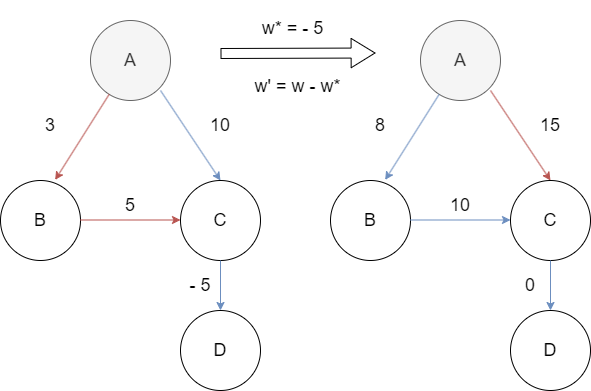
Professor Greenstreet claims that there is a simpler way to reweight edges than the method used in Johnson's algorithm. Letting $w^* = \min_{(u, v) \in E} \{w(u, v)\}$, just define $\hat w(u, v) = w(u, v) - w^*$ for all edges $(u, v) \in E$. What is wrong with the professor's method of reweighting?

Consider a graph with four vertices labeled $A$, $B$, $C$, and $D$. We want to find the shortest path from vertex $A$ to vertex $C$. Initially, there are two potential paths: $A \to B \to C$ (with 2 edges) and $A \to C$ (with a direct edge).

Introducing a reweighting factor, denoted as $w^*$, may lead to incorrect results. Reweighting could potentially make the path with more edges ($A \to B \to C$) longer than the direct edge ($A \to C$), which contradicts our goal of finding the shortest path.

25.3-5

Suppose that we run Johnson's algorithm on a directed graph $G$ with weight function $w$. Show that if $G$ contains a $0$-weight cycle $c$, then $\hat w(u, v) = 0$ for every edge $(u, v)$ in $c$.

If $\delta(s, v) - \delta(s, u) \le w(u, v)$, we have

$$\delta(s, u) \le \delta(s, v) + (0 - w(u, v)) < \delta(s, u) + w(u, v) - w(u, v) = \delta(s, u),$$

which is impossible, thus $\delta(s, v) - \delta(s, u) = w(u, v)$, $\hat w(u, v) = w(u, v) + \delta(s, u) - \delta(s, v) = 0$.

25.3-6

Professor Michener claims that there is no need to create a new source vertex in line 1 of $\text{JOHNSON}$. He claims that instead we can just use $G' = G$ and let $s$ be any vertex. Give an example of a weighted, directed graph $G$ for which incorporating the professor's idea into $\text{JOHNSON}$ causes incorrect answers. Then show that if $G$ is strongly connected (every vertex is reachable from every other vertex), the results returned by $\text{JOHNSON}$ with the professor's modification are correct.

(Removed)